‘Politics is a job that can really only be compared with navigation in uncharted waters. One has no idea how the weather or the currents will be or what storms one is in for. In politics, there is the added fact that one is largely dependent on the decisions of others, decisions on which one was counting and which then do not materialise; one’s actions are never completely one’s own. And if the friends on whose support one is relying change their minds, which is something that one cannot vouch for, the whole plan miscarries… One’s enemies one can count on – but one’s friends!’ Otto von Bismarck.
‘Everything in war is very simple, but the simplest thing is difficult. The difficulties accumulate and end by producing a kind of friction that is inconceivable unless one has experienced war… Countless minor incidents – the kind you can never really foresee – combine to lower the general level of performance, so that one always falls short of the intended goal. Iron will-power can overcome this friction … but of course it wears down the machine as well… Friction is the only concept that … corresponds to the factors that distinguish real war from war on paper. The … army and everything else related to it is basically very simple and therefore seems easy to manage. But … each part is composed of individuals, every one of whom retains his potential of friction… This tremendous friction … is everywhere in contact with chance, and brings about effects that cannot be measured… Friction … is the force that makes the apparently easy so difficult… Finally … all action takes place … in a kind of twilight, which like fog or moonlight, often tends to make things seem grotesque and larger than they really are. Whatever is hidden from full view in this feeble light has to be guessed at by talent, or simply left to chance.’ Clausewitz.
*
In July, I wrote a blog on complexity and prediction which you can read HERE.
I will summarise briefly its main propositions and add some others. All page references are to my essay, HERE. (Section 1 explores some of the maths and science issues below in more detail.)
Some people asked me after Part I – why is such abstract stuff important to practical politics? That is a big question but in a nutshell…
If you want to avoid the usual fate in politics of failure, you need to understand some basic principles about why people make mistakes and how some people, institutions, and systems cope with mistakes and thereby perform much better than most. The reason why Whitehall is full of people failing in predictable ways on an hourly basis is because, first, there is general system-wide failure and, second, everybody keeps their heads down focused on the particular and they ignore the system. Officials who speak out see their careers blow up. MPs are so cowed by the institutions and the scale of official failure that they generally just muddle along tinkering and hope to stay a step ahead of the media. Some understand the epic scale of institutional failure but they know that the real internal wiring of the system in the Cabinet Office has such a tight grip that significant improvement will be very hard without a combination of a) a personnel purge and b) a fundamental rewiring of power at the apex of the state. Many people in Westminster are now considering how this might happen. Such thoughts must, I think, be based on some general principles otherwise they are likely to miss the real causes of system failure and what to do.
In future blogs in this series, I will explore some aspects of markets and science that throw light on the question: how can humans and their institutions cope with these problems of complexity, uncertainty, and prediction in order to limit failures?
Separately, The Hollow Men II will focus on specifics of how Whitehall and Westminster work, including Number Ten and some examples from the Department for Education.
Considering the more general questions of complexity and prediction sheds light on why government is failing so badly and how it could be improved.
*
Complexity, nonlinearity, uncertainty, and prediction
Even the simplest practical problems are often very complex. If a Prime Minister wants to line up 70 colleagues in Downing Street to blame them for his woes, there are 70! ways of lining them up and 70! [70! = 70 x 69 x 68 … x 2 x 1] is roughly 10100 (a ‘googol’), which is roughly ten billion times the estimated number of atoms in the universe (1090). [See comments.]
Even the simplest practical problems, therefore, can be so complicated that searching through the vast landscape of all possible solutions is not practical.
After Newton, many hoped that perfect prediction would be possible:
‘An intellect which at a certain moment would know all the forces that animate nature, and all positions of the beings that compose it, if this intellect were vast enough to submit the data to analysis, would condense in a single formula the movements of the greatest bodies of the universe and those of the tiniest atom; for such an intellect nothing would be uncertain and the future just like the past would be present before its eyes’ (Laplace).
However, most of the most interesting systems in the world – such as brains, cultures, and conflicts – are nonlinear. That is, a small change in input has an arbitrarily large affect on output. Have you ever driven through a controlled skid then lost it? A nonlinear system is one in which you can shift from ‘it feels great on the edge’ to ‘I’m steering into the skid but I’ve lost it and might die in a few seconds’ because of one tiny input change, like your tyre catches a cat’s eye in the wet. This causes further problems for prediction. Not only is the search space so vast it cannot be searched exhaustively, however fast our computers, but in nonlinear systems one has the added problem that a tiny input change can lead to huge output changes.
Some nonlinear systems are such that no possible accuracy of measurement of the current state can eliminate this problem – there is unavoidable uncertainty about the future state. As Poincaré wrote, ‘it may happen that small differences in the initial conditions produce very great ones in the final phenomena. A small error in the former will produce an enormous error in the latter. Prediction becomes impossible, and we have the fortuitous phenomenon.’ It does not matter that the measurement error is in the 20th decimal place – the prediction will still quickly collapse.
Weather systems are like this which is why, despite the enormous progress made with predictions, we remain limited to ~10-14 days at best. To push the horizon forward by just one day requires exponential increases in the resources required. Political systems are also nonlinear. If Cohen-Blind’s aim had been very slightly different in May 1866 when he fired five bullets at Bismarck, the German states would certainly have evolved in a different way and perhaps there would have been no fearsome German army led by a General Staff into World War I, no Lenin and Hitler, and so on. Bismarck himself appreciated this very well. ‘We are poised on the tip of a lightning conductor, and if we lose the balance I have been at pains to create we shall find ourselves on the ground,’ he wrote to his wife during the 1871 peace negotiations in Versailles. Social systems are also nonlinear. Online experiments have explored how complex social networks cannot be predicted because of initial randomness combining with the interdependence of decisions.
In short, although we understand some systems well enough to make precise or statistical predictions, most interesting systems – whether physical, mental, cultural, or virtual – are complex, nonlinear, and have properties that emerge from feedback between many interactions. Exhaustive searches of all possibilities are impossible. Unfathomable and unintended consequences dominate. Problems cascade. Complex systems are hard to understand, predict and control.
Humans evolved in this complex environment amid the sometimes violent, sometimes cooperative sexual politics of small in-groups competing with usually hostile out-groups. We evolved to sense information, process it, and act. We had to make predictions amid uncertainty and update these predictions in response to feedback from our environment – we had to adapt because we have necessarily imperfect data and at best approximate models of reality. It is no coincidence that in one of the most famous speeches in history, Pericles singled out the Athenian quality of adaptation (literally ‘well-turning’) as central to its extraordinary cultural, political and economic success.
How do we make these predictions, how do we adapt? Much of how we operate depends on relatively crude evolved heuristics (rules of thumb) such as ‘sense movement >> run/freeze’. These heuristics can help. Further, our evolved nature gives us amazing pattern recognition and problem-solving abilities. However, some heuristics lead to errors, illusions, self-deception, groupthink and so on – problems that often swamp our reasoning and lead to failure.
I will look briefly at a) the success of science and mathematical models, b) the success of decentralised coordination in nature and markets, and c) the failures of political prediction and decision-making.
*
The success of science and mathematical models
Our brains evolved to solve social and practical problems, not to solve mathematical problems. This is why translating mathematical and logical problems into social problems makes them easier for people to solve (cf. Nielsen.) Nevertheless, a byproduct of our evolution was the ability to develop maths and science. Maths gives us an abstract structure of certain knowledge that we can use to build models of the world. ‘[S]ciences do not try to explain, they hardly even try to interpret, they mainly make models. By a model is meant a mathematical construct which, with the addition of certain verbal interpretations, describes observed phenomena. The justification of such a mathematical construct is solely and precisely that it is expected … correctly to describe phenomena from a reasonably wide area’ (von Neumann).
Because the universe operates according to principles that can be approximated by these models, we can understand it approximately. ‘Why’ is a mystery. Why should ‘imaginary numbers’ based on the square root of minus 1, conceived five hundred years ago and living for hundreds of years without practical application, suddenly turn out to be necessary in the 1920s to calculate how subatomic particles behave? How could it be that in a serendipitous meeting in the IAS cafeteria in 1972, Dyson and Montgomery should realise that an equation describing the distribution of prime numbers should also describe the energy level of particles? We can see that the universe displays a lot of symmetry but we do not know why there is some connection between the universe’s operating principles and our evolved brains’ abilities to do abstract mathematics. Einstein asked, ‘How is it possible that mathematics, a product of human thought that is independent of experience, fits so excellently the objects of physical reality?’ Wigner replied to Einstein in a famous paper, ‘The Unreasonable Effectiveness of Mathematics in the Natural Sciences’ (1960) but we do not know the answer. (See ‘Is mathematics invented or discovered?’, Tim Gowers, 2011.)
The accuracy of many of our models gets better and better. In some areas such as quantum physics, the equations have been checked so delicately that, as Feynman said, ‘If you were to measure the distance from Los Angeles to New York to this accuracy, it would be exact to the thickness of a human hair’. In other areas, we have to be satisfied with statistical models. For example, many natural phenomenon, such as height and intelligence, can be modelled using ‘normal distributions’. Other phenomena, such as the network structure of cells, the web, or banks in an economy, can be modelled using ‘power laws’. [* See End] Why do statistical models work? Because ‘chance phenomena, considered collectively and on a grand scale, create a non-random regularity’ (Kolmogorov). [** See End]
Science has also built an architecture for its processes, involving meta-rules, that help correct errors and normal human failings. For example, after Newton the system of open publishing and peer review developed. This encouraged scientists to make their knowledge public, confident that they would get credit (instead of hiding things in code like Newton). Experiments must be replicated and scientists are expected to provide their data honestly so that others can test their claims, however famous, prestigious, or powerful they are. Feynman described the process in physics as involving, at its best, ‘a kind of utter honesty … [Y]ou should report everything that you think might make [your experiment or idea] invalid… [Y]ou must also put down all the facts which disagree with it, as well as those that agree with it… The easiest way to explain this idea is to contrast it … with advertising.’
The architecture of the scientific process is not perfect. Example 1. Evaluation of contributions is hard. The physicist who invented the arXiv was sacked soon afterwards because his university’s tick box evaluation system did not have a way to value his enormous contribution. Example 2. Supposedly ‘scientific’ advice to politicians can also be very overconfident. E.g. A meta-study of 63 studies of the costs of various energy technologies reveals: ‘The discrepancies between equally authoritative, peer-reviewed studies span many orders of magnitude, and the overlapping uncertainty ranges can support almost any ranking order of technologies, justifying almost any policy decision as science based’ (Stirling, Nature, 12/2010).
This architecture and its meta-rules are now going through profound changes, brilliantly described by the author of the seminal textbook on quantum computers, Michael Nielsen, in his book Reinventing Discovery – a book that has many lessons for the future of politics too. But overall the system clearly has great advantages.
The success of decentralised information processing in solving complex problems
Complex systems and emergent properties
Many of our most interesting problems can be considered as networks. Individual nodes (atoms, molecules, genes, cells, neurons, minds, organisms, organisations, computer agents) and links (biochemical signals, synapses, internet routers, trade routes) form physical, mental, and cultural networks (molecules, cells, organisms, immune systems, minds, organisations, internet, biosphere, ‘econosphere’, cultures) at different scales.
The most interesting networks involve interdependencies (feedback and feedforward) – such as chemical signals, a price collapse, neuronal firing, an infected person gets on a plane, or an assassination – and are nonlinear. Complex networks have emergent properties including self-organisation. For example, the relative strength of a knight in the centre of the chessboard is not specified in the rules but emerges from the nodes of the network (or ‘agents’) operating according to the rules.
Even in physics, ‘The behavior of large and complex aggregates of elementary particles … is not to be understood in terms of a simple extrapolation of the properties of a few particles. Instead, at each level of complexity entirely new properties appear’ (Anderson). This is more obvious in biological and social networks.
Ant colonies and immune systems: how decentralised information processing solves complex problems
Ant colonies and the immune system are good examples of complex nonlinear systems with ‘emergent properties’ and self-organisation.
The body cannot ‘know’ in advance all the threats it will face so the immune system cannot be perfectly ‘pre-designed’. How does it solve this problem?
There is a large diverse population of individual white blood cells (millions produced per day) that sense threats. If certain cells detect that a threat has passed a threshold, then they produce large numbers of daughter cells, with mutations, that are tested on captured ‘enemy’ cells. Unsuccessful daughter cells die while successful ones are despatched to fight. These daughter cells repeat the process so a rapid evolutionary process selects and reproduces the best defenders and continually improves performance. Other specialist cells roam around looking for invaders that have been tagged by antibodies. Some of the cells remain in the bloodstream, storing information about the attack, to guard against future attacks (immunity).
There is a constant evolutionary arms race against bacteria and other invaders. Bacteria take over cells’ machinery and communications. They reprogram cells to take them over or trigger self-destruction. They disable immune cells and ‘ride’ them back into lymph nodes (Trojan horse style) where they attack. They shape-change fast so that immune cells cannot recognise them. They reprogram immune cells to commit suicide. They reduce competition by tricking immune cells into destroying other bacteria that help the body fight infection (e.g. by causing diarrhoea to flush out competition).
NB. there is no ‘plan’ and no ‘central coordination’. The system experiments probabilistically, reinforces success, and discards failure. It is messy. Such a system cannot be based on trying to ‘eliminate failure’. It is based on accepting a certain amount of failure but keeping it within certain tolerances via learning.
Looking at an individual ant, it would be hard to know that an ant colony is capable of farming, slavery, and war.
‘The activity of an ant colony is totally defined by the activities and interactions of its constituent ants. Yet the colony exhibits a flexibility that goes far beyond the capabilities of its individual constituents. It is aware of and reacts to food, enemies, floods, and many other phenomena, over a large area; it reaches out over long distances to modify its surroundings in ways that benefit the colony; and it has a life-span orders of magnitude longer than that of its constituents… To understand the ant, we must understand how this persistent, adaptive organization emerges from the interactions of its numerous constituents.’ (Hofstadter)
Ant colonies face a similar problem to the immune system: they have to forage for food in an unknown environment with an effectively infinite number of possible ways to search for a solution. They send out agents looking for food; those that succeed return to the colony leaving a pheromone trail which is picked up by others and this trail strengthens. Decentralised decisions via interchange of chemical signals drive job-allocation (the division of labour) in the colony. Individual ants respond to the rate of what others are doing: if an ant finds a lot of foragers, it is more likely to start foraging.
Similarities between the immune system and ant colonies in solving complex problems
Individual white blood cells cannot access the whole picture; they sample their environment via their receptors. Individual ants cannot cannot access the whole picture; they sample their environment via their chemical processors. The molecular shape of immune cells and the chemical processing abilities of ants are affected by random mutations; the way individual cells or ants respond has a random element. The individual elements (cells / ants) are programmed to respond probabilistically to new information based on the strength of signals they receive.
Environmental exploration by many individual agents coordinated via feedback signals allows a system to probe many different probabilities, reinforce success, ‘learn’ from failure (e.g withdraw resources from unproductive strategies), and keep innovating (e.g novel cells are produced even amid a battle and ants continue to look for better options even after striking gold). ‘Redundancy’ allows local failures without breaking the system. There is a balance between exploring the immediate environment for information and exploiting that information to adapt.
In such complex networks with emergent properties, unintended consequences dominate. Effects cascade: ‘they come not single spies but in battalions’. Systems defined as ‘tightly coupled‘ – that is, they have strong interdependencies so that the behaviour of one element is closely connected to another – are not resilient in the face of nonlinear events (picture a gust of wind knocking over one domino in a chain).
Network topology
We are learning how network topology affects these dynamics. Many networks (including cells, brains, the internet, the economy) have a topology such that nodes are distributed according to a power law (not a bell curve), which means that the network looks like a set of hubs and spokes with a few spokes connecting hubs. This network topology makes them resilient to random failure but vulnerable to the failure of critical hubs that can cause destructive cascades (such as financial crises) – an example of the problems that come with nonlinearity.
Similar topology and dynamics can be seen in networks operating at very different scales ranging from cellular networks, the brain, the financial system, the economy in general, and the internet. Disease networks often shows the same topology, with certain patients, such as those who get on a plane from West Africa to Europe with Ebola, playing the role of critical hubs connecting different parts of the network. Terrorist networks also show the same topology. All of these complex systems with emergent properties have the same network topology and are vulnerable to the failure of critical hubs.
Many networks evolve modularity. A modular system is one in which specific modules perform specific tasks, with links between them allowing broader coordination. This provides greater effectiveness and resilience to shocks. For example, Chongqing in China saw the evolution of a new ecosystem for designing and building motorbikes in which ‘assembler’ companies assemble modular parts built by competing companies, instead of relying on high quality vertically integrated companies like Yamaha. This rapidly decimated Japanese competition. Connections between network topology, power laws and fractals can be seen in work by physicist Geoffrey West both on biology and cities, for it is clear that just as statistical tools like the Central Limit Theorem demonstrate similar structure in completely different systems and scales, so similar processes occur in biology and social systems. [See Endnote.]
Markets: how decentralised information processing solves complex problems
[Coming imminently]
A summary of the progress brought by science and markets
The combination of reasoning, reliable accumulated knowledge, and a reliable institutional architecture brings steady progress, and occasional huge breakthroughs and wrong turns, in maths and science. The combination of the power of decentralised information processing to find solutions to complex problems and an institutional architecture brings steady progress, and occasional huge breakthroughs and wrong turns, in various fields that operate via markets.
Fundamental to the institutional architecture of markets and science is mechanisms that enable adaptation to errors. The self-delusion and groupthink that is normal for humans – being a side-effect of our nature as evolved beings – is partly countered by tried and tested mechanisms. These mechanisms are not based on an assumption that we can ‘eliminate failure’ (as so many in politics absurdly claim they will do). Instead, the assumption is that failure is a persistent phenomenon in a complex nonlinear world and it must be learned from and adapted to as quickly as possible. Entrepreneurs and scientists can be vain, go mad, or be prone to psychopathy – like public servants – but we usually catch it quicker and it causes less trouble. Catching errors, we inch forward ‘standing on the shoulders of giants’ as Newton put it.
Science has enabled humans to make transitions from numerology to mathematics, from astrology to astronomy, from alchemy to chemistry, from witchcraft to neuroscience, from tallies to quantum computation. Markets have been central to a partial transition in a growing fraction of the world from a) small, relatively simple, hierarchical, primitive, zero-sum hunter-gatherer tribes based on superstition (almost total ignorance of complex systems), shared aims, personal exchange and widespread violence, to b) large, relatively complex, decentralised, technological, nonzero-sum market-based cultures based on science (increasingly accurate predictions and control in some fields), diverse aims, impersonal exchange, trade, private property, and (roughly) equal protection under the law.
*
The failures of politics: wrong predictions, no reliable mechanisms for fixing obvious errors
‘No official estimates even mentioned that the collapse of Communism was a distinct possibility until the coup of 1989.’ National Security Agency, ‘Dealing With the Future’, declassified report.
However, the vast progress made in so many fields is clearly not matched in standards of government. In particular, it is very rare for individuals or institutions to make reliable predictions.
The failure of prediction in politics
Those in leading positions in politics and public service have to make all sorts of predictions. Faced with such complexity, politicians and others have operated mostly on heuristics (‘political philosophy’), guesswork, willpower and tactical adaptation. My own heuristics for working in politics are: focus, ‘know yourself’ (don’t fool yourself), think operationally, work extremely hard, don’t stick to the rules, and ask yourself ‘to be or to do?’.
Partly because politics is a competitive enterprise in which explicit and implicit predictions elicit countermeasures, predictions are particularly hard. This JASON report (PDF) on the prediction of rare events explains some of the technical arguments about predicting complex nonlinear systems such as disasters. Unsurprisingly, so-called ‘political experts’ are not only bad at predictions but are far worse than they realise. There are many prominent examples. Before the 2000 election, the American Political Science Association’s members unanimously predicted a Gore victory. Beyond such examples, we have reliable general data on this problem thanks to a remarkable study by Philip Tetlock. He charted political predictions made by supposed ‘experts’ (e.g will the Soviet Union collapse, will the euro collapse) for fifteen years from 1987 and published them in 2005 (‘Expert Political Judgement’). He found that overall, ‘expert’ predictions were about as accurate as monkeys throwing darts at a board. Experts were very overconfident: ~15 percent of events that experts claimed had no chance of occurring did happen, and ~25 percent of those that they said they were sure would happen did not happen. Further, the more media interviews an expert did, the less likely they were to be right. Specific expertise in a particular field was generally of no value; experts on Canada were about as accurate on the Soviet Union as experts on the Soviet Union were.
However, some did better than others. He identified two broad categories of predictor. The first he called ‘hedgehogs’ – fans of Big Ideas like Marxism, less likely to admit errors. The second he called ‘foxes’ – not fans of Big Ideas, more likely to admit errors and change predictions because of new evidence. (‘The fox knows many little things, but the hedgehog knows one big thing,’ Archilochus.) Foxes tended to make better predictions. They are more self-critical, adaptable, cautious, empirical, and multidisciplinary. Hedgehogs get worse as they acquire more credentials while foxes get better with experience. The former distort facts to suit their theories; the latter adjust theories to account for new facts.
Tetlock believes that the media values characteristics (such as Big Ideas, aggressive confidence, tenacity in combat and so on) that are the opposite of those prized in science (updating in response to new data, admitting errors, tenacity in pursuing the truth and so on). This means that ‘hedgehog’ qualities are more in demand than ‘fox’ qualities, so the political/media market encourages qualities that make duff predictions more likely. ‘There are some academics who are quite content to be relatively anonymous. But there are other people who aspire to be public intellectuals, to be pretty bold and to attach non-negligible probabilities to fairly dramatic change. That’s much more likely to bring you attention’ (Tetlock).
Tetlock’s book ought to be much-studied in Westminster particularly given 1) he has found reliable ways of identifying a small number of people who are very good forecasters and 2) IARPA (the intelligence community’s DARPA twin) is working with Tetlock to develop training programmes to improve forecasting skills. [See Section 6.] Tetolock says, ‘We now have a significant amount of evidence on this, and the evidence is that people can learn to become better. It’s a slow process. It requires a lot of hard work, but some of our forecasters have really risen to the challenge in a remarkable way and are generating forecasts that are far more accurate than I would have ever supposed possible from past research in this area.’ (This is part of IARPA’s ACE programme to develop aggregated forecast systems and crowdsourced prediction software. IARPA also has the SHARP programme to find ways to improve problem-solving skills for high-performing adults.)
His main advice? ‘If I had to bet on the best long-term predictor of good judgement among the observers in this book, it would be their commitment – their soul-searching Socratic commitment – to thinking about how they think’ (Tetlock). His new training programmes help people develop this ‘Socratic commitment’ and correct their mistakes in quite reliable ways.
NB. The extremely low quality of political forecasting is what allowed an outsider like Nate Silver to transform the field simply by applying some well-known basic maths.
The failure of prediction in economics
‘… the evidence from more than fifty years of research is conclusive: for a large majority of fund managers, the selection of stocks is more like rolling dice than like playing poker. Typically at least two out of every three mutual funds underperform the overall market in any given year. More important, the year-to-year correlation between the outcomes of mutual funds is very small, barely higher than zero. The successful funds in any given year are mostly lucky; they have a good roll the dice.’ Daniel Kahneman, winner of the economics ‘Nobel’ (not the same as the Nobel for physical sciences).
‘I importune students to read narrowly within economics, but widely in science…The economic literature is not the best place to find new inspiration beyond these traditional technical methods of modelling’ Vernon Smith, winner of the economics ‘Nobel’.
I will give a few examples of problems with economic forecasting.
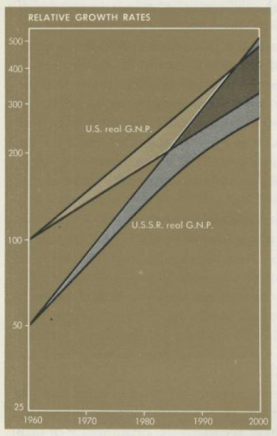
In the 1961 edition of his famous standard textbook used by millions of students, one of the 20th Century’s most respected economists, Paul Samuelson, predicted that respective growth rates in America and the Soviet Union meant the latter would overtake the USA between 1984-1997. By 1980, he had delayed the date to be in 2002-2012. Even in 1989, he wrote, ‘The Soviet economy is proof that, contrary to what many skeptics had earlier believed, a socialist command economy can function and even thrive.’
Chart: Samuelson’s prediction for the Soviet economy
The recent financial crisis also demonstrated many failed predictions. Various people, including physicists Steve Hsu and Eric Weinstein, published clear explanations of the extreme dangers in the financial markets and parallels with previous crashes such as Japan’s. However, they were almost totally ignored by politicians, officials, central banks and so on. Many of those involved were delusional. Perhaps most famously, Joe Cassano of AIG Financial said in a conference call (8/2007): ‘It’s hard for us – without being flippant – to even see a scenario within any kind of realm of reason that would see us losing one dollar in any of those transactions… We see no issues at all emerging.’
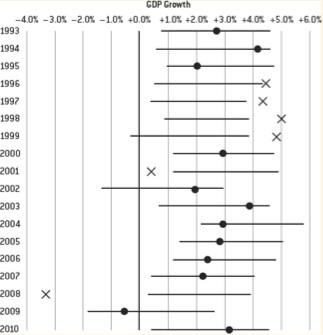
Nate Silver recently summarised some of the arguments over the crash and its aftermath. In December 2007, economists in the Wall Street Journal forecasting panel predicted only a 38 percent chance of recession in 2008. The Survey of Professional Forecasters is a survey of economists’ predictions done by the Federal Reserve Bank that includes uncertainty measurements. In November 2007, the Survey showed a net prediction by economists that the economy would grow by 2.4% in 2008, with a less than 3% chance of any recession and a 1-in-500 chance of it shrinking by more than 2%.
Chart: the 90% ‘prediction intervals’ for the Survey of Professional Forecasters net forecast of GDP growth 1993-2010
If the economists’ predictions were accurate, the 90% prediction interval should be right nine years out of ten, and 18 out of 20. Instead, the actual growth was outside the 90% prediction interval six times out of 18, often by a lot. (The record back to 1968 is worse.) The data would later reveal that the economy was already in recession in the last quarter of 2007 and, of course, the ‘1-in-500’ event of the economy shrinking by more than 2% is exactly what happened.**
Although the total volume of home sales in 2007 was only ~$2 trillion, Wall Street’s total volume of trades in mortgage-backed securities was ~$80 trillion because of the creation of ‘derivative’ financial instruments. Most people did not understand 1) how likely a house price fall was, 2) how risky mortgage-backed securities were, 3) how widespread leverage could turn a US housing crash into a major financial crash, and 4) how deep the effects of a major financial crash were likely to be. ‘The actual default rates for CDOs were more than two hundred times higher than S&P had predicted’ (Silver). In the name of ‘transparency’, S&P provided the issuers with copies of their ratings software allowing CDO issuers to experiment on how much junk they could add without losing a AAA rating. S&P even modelled a potential housing crash of 20% in 2005 and concluded its highly rated securities could ‘weather a housing downturn without suffering a credit rating downgrade.’
Unsurprisingly, Government unemployment forecasts were also wrong. Historically, the uncertainty in an unemployment rate forecast made during a recession had been about plus or minus 2 percent but Obama’s team, and economists in general, ignored this record and made much more specific predictions. In January 2009, Obama’s team argued for a large stimulus and said that, without it, unemployment, which had been 7.3% in December 2008, would peak at ~9% in early 2010, but with the stimulus it would never rise above 8% and would fall from summer 2009. However, the unemployment numbers after the stimulus was passed proved to be even worse than the ‘no stimulus’ prediction. Similarly, the UK Treasury’s forecasts about growth, debt, and unemployment from 2007 were horribly wrong but that has not stopped it making the same sort of forecasts.
Paul Krugman concluded from this episode: the stimulus was too small. Others concluded it had been a waste of money. Academic studies vary widely in predicting the ‘return’ from each $1 of stimulus. Since economists cannot even accurately predict a recession when the economy is already in recession, it seems unlikely that there will be academic consensus soon on such issues. Economics often seems like a sort of voodoo for those in power – spurious precision and delusions that there are sound mathematical foundations for the subject without a proper understanding of the conditions under which mathematics can help (cf. Von Neumann on maths and prediction in economics HERE).
Fields which do better at prediction
Daniel Kahneman, who has published some of the most important research about why humans make bad predictions, summarises the fundamental issues about when you can trust expert predictions:
‘To know whether you can trust a particular intuitive judgment, there are two questions you should ask: Is the environment in which the judgment is made sufficiently regular to enable predictions from the available evidence? The answer is yes for diagnosticians, no for stock pickers. Do the professionals have an adequate opportunity to learn the cues and the regularities? The answer here depends on the professionals’ experience and on the quality and speed with which they discover their mistakes. Anesthesiologists have a better chance to develop intuitions than radiologists do. Many of the professionals we encounter easily pass both tests, and their off-the-cuff judgments deserve to be taken seriously. In general, however, you should not take assertive and confident people at their own evaluation unless you have independent reason to believe that they know what they are talking about.’ (Emphasis added.)
It is obvious that politics fulfils neither of his two criteria – it does not even have hard data and clear criteria for success, like stock picking.
I will explore some of the fields that do well at prediction in a future blog.
*
The consequences of the failure of politicians and other senior decision-makers and their institutions
‘When superior intellect and a psychopathic temperament coalesce …, we have the best possible conditions for the kind of effective genius that gets into the biographical dictionaries’ (William James).
‘We’re lucky [the Unabomber] was a mathematician, not a molecular biologist’ (Bill Joy, Silicon Valley legend, author of ‘Why the future doesn’t need us’).
While our ancestor chiefs understood bows, horses, and agriculture, our contemporary chiefs (and those in the media responsible for scrutiny of decisions) generally do not understand their equivalents, and are often less experienced in managing complex organisations than their predecessors.
The consequences are increasingly dangerous as markets, science and technology disrupt all existing institutions and traditions, and enhance the dangerous potential of our evolved nature to inflict huge physical destruction and to manipulate the feelings and ideas of many people (including, sometimes particularly, the best educated) through ‘information operations’. Our fragile civilisation is vulnerable to large shocks and a continuation of traditional human politics as it was during 6 million years of hominid evolution – an attempt to secure in-group cohesion, prosperity and strength in order to dominate or destroy nearby out-groups in competition for scarce resources – could kill billions. We need big changes to schools, universities, and political and other institutions for their own sake and to help us limit harm done by those who pursue dreams of military glory, ‘that attractive rainbow that rises in showers of blood’ (Lincoln).
The global population of people with an IQ four standard deviations above the average (i.e. >160) is ~250k. About 1% of the population are psychopaths so there are perhaps ~2-3,000 with IQ ≈ Nobel/Fields winner. The psychopathic +3SD IQ (>145; average science PhD ~130) population is 30 times bigger. A subset will also be practically competent. Some of them may think, ‘Flectere si nequeo superos, / Acheronta movebo’ (‘If Heav’n thou can’st not bend, Hell thou shalt move’, the Aeneid). Board et al (2005) showed that high-level business executives are more likely than inmates of Broadmoor to have one of three personality disorders (PDs): histrionic PD, narcissistic PD, and obsessive-compulsive PD. Mullins-Sweatt et al (2010) showed that successful psychopaths are more conscientious than the unsuccessful.
A brilliant essay (here) by one of the 20th Century’s best mathematicians, John von Neumann, describes these issues connecting science, technology, and how institutions make decisions.
*
Some conclusions
When we consider why institutions are failing and how to improve them, we should consider the general issues discussed above. How to adapt quickly to new information? Does the institution’s structure incentivise effective adaptation or does it incentivise ‘fooling oneself’ and others? Is it possible to enable distributed information processing to find a ‘good enough’ solution in a vast search space? If your problem is similar to that of the immune system or ant colony, why are you trying to solve it with a centralised bureaucracy?
Further, some other obvious conclusions suggest themselves.
We could change our society profoundly by dropping the assumption that less than a tenth of the population is suitable to be taught basic concepts in maths and physics that have very wide application to our culture, such as normal distributions and conditional probability. This requires improving basic maths 5-16 and it also requires new courses in schools.
One of the things that we did in the DfE to do this was work with Fields Medallist Tim Gowers on a sort of ‘Maths for Presidents’ course. Professor Gowers wrote a fascinating blog on this course which you can read HERE. The DfE funded MEI to develop the blog into a real course. This has happened and the course is now being developed in schools. Physics for Future Presidents already exists and is often voted the most popular course at UC Berkeley (Cf. HERE). School-age pupils, arts graduates, MPs, and many Whitehall decision-makers would greatly benefit from these two courses.
We also need new inter-disciplinary courses in universities. For example, Oxford could atone for PPE by offering Ancient and Modern History, Physics for Future Presidents, and How to Run a Start Up. Such courses should connect to the work of Tetlock on The Good Judgement Project, as described above (I will return to this subject).
Other countries have innovated successfully in elite education. For example, after the shock of the Yom Kippur War, Israel established the ‘Talpiot’ programme which ‘aims to provide the IDF and the defense establishment with exceptional practitioners of research and development who have a combined understanding in the fields of security, the military, science, and technology. Its participants are taught to be mission-oriented problem-solvers. Each year, 50 qualified individuals are selected to participate in the program out of a pool of over 7,000 candidates. Criteria for acceptance include excellence in physical science and mathematics as well as an outstanding demonstration of leadership and character. The program’s training lasts three years, which count towards the soldiers’ three mandatory years of service. The educational period combines rigorous academic study in physics, computer science, and mathematics alongside intensive military training… During the breaks in the academic calendar, cadets undergo advanced military training… In addition to the three years of training, Talpiot cadets are required to serve an additional six years as a professional soldier. Throughout this period, they are placed in assorted elite technological units throughout the defense establishment and serve in central roles in the fields of research and development’ (IDF, 2012). The programme has also helped the Israeli hi-tech economy.****
If politicians had some basic training in mathematical reasoning, they could make better decisions amid complexity. If politicians had more exposure to the skills of a Bill Gates or Peter Thiel, they would be much better able to get things done.
I will explore the issue of training for politicians in a future blog.
Please leave corrections and comments below.
* It is very important to realise when the system one is examining is well approximated by a normal distribution and when by a power law. For example… When David Viniar (Goldman Sachs CFO) said of the 2008 financial crisis, ‘We were seeing things that were 25-standard-deviation events, several days in a row,’ he was discussing financial prices as if they can be accurately modelled by a normal distribution, and implying that events that should happen once every 10135 years (the Universe is only ~1.4×1010 years old) were occurring ‘several days in a row’. He was either ignorant of basic statistics (unlikely) or taking advantage of the statistical ignorance of his audience. Actually, we have known for a long time that financial prices are not well modelled using normal distributions because they greatly underestimate the likelihood of bubbles and crashes. If politicians don’t know what ‘standard deviation’ means, it is obviously impossible for them to contribute much to detailed ideas on how to improve bank regulation. It is not hard to understand standard deviation and there is no excuse for this situation to continue for another generation.
** However, there is also a danger in the use of statistical models based on ‘big data’ analysis – ‘overfitting’ models and wrongly inferring a ‘signal’ from what is actually ‘noise’. We usually a) have a noisy data set and b) an inadequate theoretical understanding of the system, so we do not know how accurately the data represents some underlying structure (if there is such a structure). We have to infer a structure despite these two problems. It is easy in these circumstances to ‘overfit’ a model – to make it twist and turn to fit more of the data than we should, but then we are fitting it not to the signal but to the noise. ‘Overfit’ models can seem to explain more of the variance in the data – but they do this by fitting noise rather than signal (Silver, op. cit).
This error is seen repeatedly in forecasting, and can afflict even famous scientists. For example, Freeman Dyson tells a short tale about how, in 1953, he trekked to Chicago to show Fermi the results of a new physics model for the strong nuclear force. Fermi dismissed his idea immediately as having neither ‘a clear physical picture of the process that you are calculating’ nor ‘a precise and self-consistent mathematical formalism’. When Dyson pointed to the success of his model, Fermi quoted von Neumann, ‘With four parameters I can fit an elephant, and with five I can make him wiggle his trunk’, thus saving Dyson from wasting years on a wrong theory (A meeting with Enrico Fermi, by Freeman Dyson). Imagine how often people who think they have a useful model in areas not nearly as well-understood as nuclear physics lack a Fermi to examine it carefully.
There have been eleven recessions since 1945 but people track millions of statistics. Inevitably, people will ‘overfit’ many of these statistics to model historical recessions then ‘predict’ future ones. A famous example is the Superbowl factor. For 28 years out of 31, the winner of the Superbowl correctly ‘predicted’ whether the stock exchange rose or fell. A standard statistical test ‘would have implied that there was only about a 1-in-4,700,000 possibility that the relationship had emerged from chance alone.’ Just as someone will win the lottery, some arbitrary statistics will correlate with the thing you are trying to predict just by chance (Silver)
*** Many of these wrong forecasts were because the events were ‘out of sample’. What does this mean? Imagine you’ve taken thousands of car journeys and never had a crash. You want to make a prediction about your next journey. However, in the past you have never driven drunk. This time you are drunk. Your prediction is therefore out of sample. Predictions of US housing data were based on past data but there was no example of such huge leveraged price rises in the historical data. Forecasters who looked at Japan’s experience in the 1980’s better realised the danger. (Silver)
**** The old Technical Faculty of the KGB Higher School (rebaptised after 1991) ran similar courses; one of its alumni is Yevgeny Kaspersky, whose company first publicly warned of the cyberweapons Stuxnet and Flame (and who still works closely with his old colleagues). It would be interesting to collect information on elite intelligence and special forces training programmes. E.g. Post-9/11, US special forces (acknowledged and covert) have greatly altered including adding intelligence roles that were previously others’ responsibility or regarded as illegal for DOD employees. How does what is regarded as ‘core training’ for such teams vary, how is it changing, and why are some better than others at decisions under pressure and surviving disaster?
Dominic,
Not that it’ll matter to most of your readers, but I think you’ve just made the observable universe at least five million (maybe as much as fifty billion) times bigger, in terms of numbers of atoms or nucleons (most of it being hydrogen), than the generally accepted figure (10^78 to 10^82, or let’s make it <= ~ 2×10^83, to allow, in a rough 'n ready way for dark matter).
http://www.kurzweilai.net/the-computational-universe-2 quotes Seth Lloyd as writing "The amount of information you could process if you were to use all the energy and matter of the universe is 10^90 bits". Perhaps that was what you were referring to?
Regardless – enjoy your blogs – keep 'em coming
LikeLike
Thanks. I can’t remember where I saw the 10^90 figure – though I did read Seth Lloyd’s book – but looking around the web you are clearly right, people seem to use ~10^80.
So if one uses ~10^80, then 70! ≈ 10^100 ≈ 10^20 times the estimated number of atoms in the universe (not 10^10) so it’s even bigger!
Thanks for taking the trouble to correct this.
D
LikeLike
Hi, I think some of what you ascribe to bacteria iscactually virus behaviour ( cell hijacking), but I am delighted to know there is somewhere else out there who knows the implications of the Centra Limit Theorem and Mandelbrot’s work.
BTW, have you come across Eli Goldratt’s work on how to make change in an organisation ? It is popularly known as TOC or ‘Theory of Constraints’. There is a story about Goldratt and officials at the DoH I might share with you one day.
LikeLike
However, being the Fermi in your organisation doesn’t win friends or plaudits…..(an effective leader always listens to their fearless Fermis)….
LikeLike
Pingback: The Hollow Men II: Some reflections on Westminster and Whitehall dysfunction | Dominic Cummings's Blog
Pingback: On the Referendum #3: The errors of Steve Richards | Dominic Cummings's Blog
Pingback: The Hollow Men II: Some reflections on Westminster and Whitehall dysfunction | Dominic Cummings's Blog
Pingback: On the Referendum #5: reports of an anti-EU advertising campaign; Greece, the euro, and predictions | Dominic Cummings's Blog
This is a cracking blog, but I think it’s worth pointing out that the lack of basic understanding of statistics actually extends to many of the advisers who purport to have expertise in that field.
That is quite dangerous when politicians rely on advisers who put together superficially convincing models and mathematical justifications for actions, which they basically don’t understand themselves.
I think (speculate) that some of the following may be relevant:
1. The British culture of treating postgraduate education as an optional extra for rich lazy people or unemployable intellectuals. If we want our brightest and best to really understand multiple disciplines in sufficient depth, then they will have to spend more time studying. We may want to “professionalise” certain fields by requiring higher levels of qualifications. A good starting point would be market research, which drives a lot of political decisions, and is an industry absolutely teeming with unqualified chancers. A side effect might be that academia itself would become more competitive and there would be less of the “progression by default” that you get in the social sciences, with very weak thinkers becoming professors of politics.
2. An oversized finance sector attracting too many of the best mathematical and scientific minds (particularly the rare ones who can apply their mathematical prowess to complex real-world problems). It is so rare in London that you meet a mathematically capable person who doesn’t work in finance. It shouldn’t be that way.
3. An overreliance on exporting the English language. By this I mean many British companies are viable because they export a crap service in excellent prose, in an international language. Far too many so-called “businessmen” who become MPs and politicos have only really experienced business success with a venture like this (PR, comms, media, etc.). It is hardly comparable with setting up a successful manufacturing business, or a genuinely innovative tech start-up.
4. Libel laws and weak whistleblower protections which shield snake oil salesmen from robust critique. Many of Britain’s most successful businesses are essentially clever scams – at least part of the time. Hedge funds may or may not beat the market, but they always make money from their clients; management consultancies may or may not add some value to a process, but they always make money from their (often government) clients; and so on and so forth. We need to give individuals the power to blow these cosy deals open – they are anti-market and they offer perverse incentives to clever people to do stupid, unproductive things.
5. A media (including so-called public service broadcasters) which can only “popularise” science, whereas it often attempts to do politics, history, and economics seriously. Listen to Melvin Bragg’s In Our Time on a historical or philosophical question, and the discussion flows freely. But on the recent P versus NP programme, he got completely lost and tried to look for popular angles. He is a Radio 4 intellectual – it only gets worse from that point downwards. Indeed, some of the best TV coverage of complex systems comes via sport – people like Clive Woodward, Gary Neville, and David Coulthard have a sophisticated understanding of complex systems in their respective sports. Of course, they are in a minority, as TV still prefers to pair them with entertaining morons.
6. London. George Osborne’s best idea (on paper) is the Northern Powerhouse. Let’s see what happens. But really we need competition between cities to drive different ways of thinking about Britain’s political future. The rise of San Francisco and Silicon Valley has had a transformative effect on aspects of American politics (unfortunately coinciding with other trends that have had very negative effects). But it’s hard to see where this transformative change happens in the UK.
7. Our lack of foreign languages. This is actually a very tricky one – it is tough learning a foreign language as an English speaker, because foreigners insist on speaking English to you, and the short-term incentives are very weak. But in the long term, I think it is preventing us from engaging with diverse sets of ideas. Germany has a rich intellectual history that is virtually unknown in the UK. We need a larger subset of our population to engage properly with China, Russia, India – this would have the side effect of exposing us to the importance these cultures place on STEM subjects.
8. We somehow need to make STEM subject expertise a cultural aspiration, and I think the only way to do that is to promote the renaissance (wo)man – the multidisciplinary intellectual – as a cultural ideal. But that means really stamping down hard on the faux intellectual – the well-spoken classicist or historian or musician who can’t do maths. Because if you can’t do maths, you shouldn’t really be talking about *anything* that involves cause and effect.
LikeLiked by 2 people
Excellent comment, thanks
D
LikeLike
I am pleased I found your blog.
LikeLike
Thanks, tell a friend…
D
LikeLike
It seems Mr Elon Musk is implementing some form of a crowdsourced media evaluation tool. I just hope he has read Tetlock!
LikeLike